Der erweiterte euklidische Algorithmus ist ein Algorithmus, der den größten gemeinsamen Teiler von zwei Zahlen bestimmt (den ggT) und zusätzlich die sogenannten Bézout-Koeffizienten für diese zwei Zahlen sehr effizient berechnen kann. Die Bézout-Koeffizienten "s" und "t" der Zahlen "n" und "m" erfüllen folgende Beziehung:

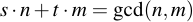
latex:s \* n + t \* m = \textnormal{gcd}(n, m)

Hierbei steht "gcd" für greatest common divisor, also größter gemeinsamer Teiler. Falls der ggT von "n" und "m" 1 ist, haben die Bézout-Koeffizienten eine besondere Bedeutung: in den beiden Ringen Zn und Zm sind jeweils "s" und "t" die multiplikativen inversen Elemente von m und n. Es gilt also:

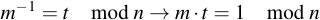
latex:m^{-1} = t \mod n \rightarrow m \* t = 1 \mod n
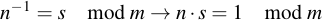
latex:n^{-1} = s \mod m \rightarrow n \* s = 1 \mod m

A B Q R S T U V Berechnung
60 7 1 0 0 1 Startwerte
60 7 8 4 Q = A / B = 60 / 7 = 8
R = A % B = 60 % 7 = 4
60 7 8 4 0 1 S = Ualt = 0
T = Valt = 1
60 7 8 4 0 1 1 -8 U = Salt - (Q · Ualt) = 1 - (8 · 0) = 1
V = Talt - (Q · Valt) = 0 - (8 · 1) = -8
60 7 8 4 0 1 1 -8 Q = A / B = 60 / 7 = 8
R = A % B = 60 % 7 = 4
S = Ualt = 0
T = Valt = 1
U = Salt - (Q · Ualt) = 1 - (8 · 0) = 1
V = Talt - (Q · Valt) = 0 - (8 · 1) = -8
7 4 A = Balt = 7
B = R = 4
7 4 1 3 Q = A / B = 7 / 4 = 1
R = A % B = 7 % 4 = 3
7 4 1 3 1 -8 S = Ualt = 1
T = Valt = -8
7 4 1 3 1 -8 -1 9 U = Salt - (Q · Ualt) = 0 - (1 · 1) = -1
V = Talt - (Q · Valt) = 1 - (1 · -8) = 9
7 4 1 3 1 -8 -1 9 Q = A / B = 7 / 4 = 1
R = A % B = 7 % 4 = 3
S = Ualt = 1
T = Valt = -8
U = Salt - (Q · Ualt) = 0 - (1 · 1) = -1
V = Talt - (Q · Valt) = 1 - (1 · -8) = 9
4 3 A = Balt = 4
B = R = 3
4 3 1 1 Q = A / B = 4 / 3 = 1
R = A % B = 4 % 3 = 1
4 3 1 1 -1 9 S = Ualt = -1
T = Valt = 9
4 3 1 1 -1 9 2 -17 U = Salt - (Q · Ualt) = 1 - (1 · -1) = 2
V = Talt - (Q · Valt) = -8 - (1 · 9) = -17
4 3 1 1 -1 9 2 -17 Q = A / B = 4 / 3 = 1
R = A % B = 4 % 3 = 1
S = Ualt = -1
T = Valt = 9
U = Salt - (Q · Ualt) = 1 - (1 · -1) = 2
V = Talt - (Q · Valt) = -8 - (1 · 9) = -17
3 1 A = Balt = 3
B = R = 1
3 1 3 0 Q = A / B = 3 / 1 = 3
R = A % B = 3 % 1 = 0
3 1 3 0 2 -17 S = Ualt = 2
T = Valt = -17
1 2 -17 Endergebnis

Ergebnis:
ggT(60, 7) = 1
2 · 60 + -17 · 7 = ggT(60, 7) = 1

Die Zahl 2 ist das multiplikative inverse Element von 60 im Ring Z7, also 60 · 2 = 120 = 1 mod 7.

Die Zahl -17 ist das multiplikative inverse Element von 7 im Ring Z60, also 7 · -17 = -119 = 1 mod 60.
-17 ist gleich 43 mod 60, daher gilt natürlich auch: 43 ist das multiplikative inverse Element von 7 im Ring Z60, also 7 · 43 = 301 = 1 mod 60.